Fd smectic

Low magnification microphotograph of the smectic phase (top) in coexistence with the cholesteric phase (bottom). The periodicity of the pitch is about 30 microns.	Optical micrographs of a smectic phase of four M13 virus mutants. The virus particles lie in the plane of the sample, and the long axis of the molecules lies perpendicular to the parallel lines. The periodicity of the smectic is about 0.4 microns (a), 0.7 microns (b), 0.9 microns (c), and 1.25 microns (d) corresponding to 4 viruses of length 0.39, 0.66, 0.88, and 1.2 microns, respectively.

Twist grain boundaries of smectic phase:

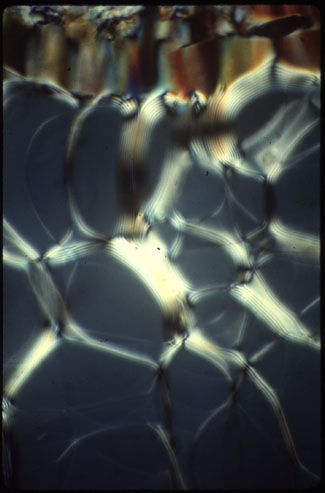
Figures (a-f) are optical micrographs of a smectic phase of fd virus molecules. The fd particles lie in the plane of the sample, and the long axis of the molecules lies perpendicular to the parallel lines in Fig (a). The periodicity of the smectic is about 0.9 microns.

A smectic resists the twist deformation because it destroys the layering, thus defects must be introduced when such a deformation is imposed. Under a twist strain, a smectic can respond by either accommodating the twist all at once by locally melting the smectic (analogous to a normal-Type I superconductor transition induced by a magnetic field), or by introducing a periodic array of defects and distributing the twist in discrete increments throughout the sample (analogous to the Abrikosov flux lattice in a Type II). Which behavior is observed depends on the relative cost of creating a smectic - nematic interface versus the cost of producing screw dislocations.

Shown in the above images are video enhanced DIC optical micrographs of textures in a fd smectic with the layers oriented normal to the slides (the ``bookshelf'' geometry), which is uniformly twisted between the top and bottom slides that contain it. In the superconducting analogy, this is equivalent to imposing a magnetic field on a superconductor. The spatial resolution and depth of field of the images are 0.2 microns. With serial images at different depths in a sample, we can map out the detailed three dimensional spatial configuration of the smectic layers, and Figure (a-e) are a series of images separated in depth by 0.5 microns. The imposed twist is accommodated in the smectic by taking the form of a series of regularly spaced blocks of smectics with a constant angle of rotation between adjacent blocks. Although only three blocks are shown in Figs. a, c, and e, this pattern persisted throughout the 5 micron thick sample. Inbetween each block are expected a series of regularly spaced twist grain boundaries (TGB). However, the structure in the plane of the screw dislocations cannot be seen because of the finite depth of field of the microscope. Instead, when focused at the interface between smectic blocks we observe a Moire pattern from the blocks above and below the focus plane (Figs b and d). This sets an upper limit on the thickness of the grain boundary of less than 0.2 microns and establishes that the blocks rotate in discrete amounts, as expected for the TGB texture.

• Fraden, S. "Phase Transitions in Colloidal Suspensions of Virus Particles." In: Observation, Prediction, and Simulation of Phase Transitions in Complex Fluids, edited by Baus, M., Rull, L.F., and Ryckaert, J.P. NATO ASI Series C 460, Kluwer Academic Publishers, 1995,p. 113-164.

• Dogic, Z. and Fraden, S. "Smectic phase in a colloidal suspension of semiflexible virus particles." Phys.Rev.Letts. 78:2417-2420, 1997.