Fraden Group

The coordination number of granular cylinders

(selected as an editorial board highlight of Europhysics Letters, 2006)

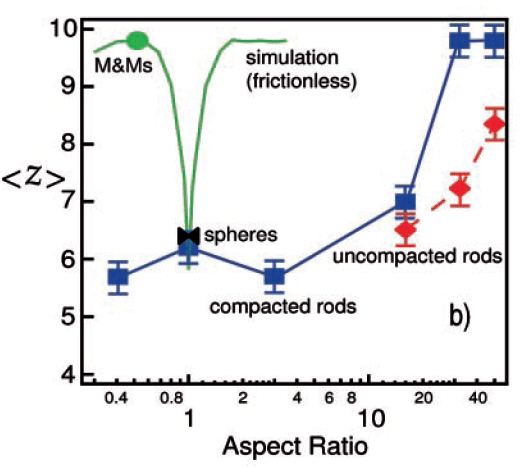
In any packing of granular material the coordination number, or number of touching neighbors per particle, is an important quantity because contacts between particles in a pile provide the necessary mechanical constraints to ensure a stable pile. Although the majority of granular studies concentrate on spheres, in Nature granular material is almost always aspherical, which motivated us to make the first measurements of the coordination number distribution for random packings of right cylindrical granular particles as a function of the rod length (L) to diameter (D), or aspect ratio, for both rods (L/D > 1) and disks (L/D < 1).

Donev et al. performed simulations of random packings of frictionless ellipsoids showing that <z> has a minimum for spheres (aspect ratio one) and increases continuously as spheres are deformed into either prolate or oblate ellipsoids from <z> ~ 6 for spheres to <z> ~ 10 for maximally jammed random packings of prolate or oblate ellipsoids at aspect ratios of approximately two and one-half, respectively.

These results contradict the isostatic conjecture arising from constraint and force balance arguments, which predict that <z> jumps discontinuously from <z> = 6 to <z> = 10 when frictionless spheres are infinitesimally deformed into ellipsoids. If the isostatic conjecture gives too high a value for the lower limit of <z>, then what is wrong with the conjecture? Donev et al. provide an example of ellipses which are locally jammed with fewer contacts than predicted in which the contact normals are correlated such that the normals intersect. A more complete explanation is that near spheres need only 2d neighbors to block translations and if the radii of curvature at the point of contact are flat enough then rotations are blocked as well. Thus Donev et al. predict for prolate ellipsoids that . Although the lower limit on <z> given by the enumeration argument is wrong for nearly spherical ellipsoids, is the lower limit also wrong for cylinders, which unlike ellipsoids do not have a spherical limit at L/D = 1?

Thus for right cylinders we expected that <z> ~ 10 for all aspect ratios. Instead, we were surprised to find that <z> ~ 6 for cylinders of L/D ~ 1. This could be due to friction, however we do not observe that <z> varied as a function of friction, rather <z> varied as a function of L/D. Finally we note that prolate ellipsoids (the candy M&M's) gave a value of <z> ~ 10, while for right cylindrical disks of similar aspect ratio we observed <z> ~ 6. In contradiction to the isostatic conjecture, it seems that shape plays a more significant role than symmetry in determining the average contact number <z>.